Puusepa matemaatika

Sissejuhatus

Matemaatikat õppides võib tihti juhtuda nii, et tehakse läbi küll arvutused, kui ei mõtestata enda jaoks lahti olukorda, kus seda teadmist tegelikus elus võib vaja minna. Üheks selliseks valdkonnaks võiks tuua geomeetriliste kehade suuruste (pindala, ruumala, nurgad) arvutamine, kus see on palju seotud meie igapäevaelu ja tööga.

Praktilises elus on aga sellel suur tähtsus, kuna me arvutame näiteks tükitöö puhul välja oma palkasid (pinnad, ruumalad), samuti materjalide tellimisel peab meil olema selge mahtude arvutamise (risttahukad, kolmnurgad, püramiidid, silindrid jne.) oskus.

Et seda kõike võimalik eelnevalt planeerides teha oleks on vaja jooniseid (projekti).

Kui alustada küsimusega, miks läheb ehitajatel vaja jooniseid, siis vastuseid võib olla erinevaid? Kuid üheks peamiseks põhjuseks on esiteks planeeritavast ehitisest ettekujutuse saamine. Nimelt, kui alustada ehitamist, siis on võimalik loodusesse paigaldada projekti alusel objekt; projekteerimise kaudu saadaksegi on juba eelnevalt läbimõeldud ja mõtestatud tulemus, millel on kindlad mõõdud ja suurus.

Juhul, kui kasutatakse ehitise püstitamiseks professionaalsete ehitajate abi, siis ehitise tellijal on eelpool nimetatule projekti kaudu võimalik väga konkreetselt ja selgelt edasi anda oma soov ja nägemus planeeritavast tulevikuvisioonist.

Kogus selline tegevus toimub igapäevaelus lihtsate matemaatiliste tehete kaudu. Seega on käesolev õppematerjal mõeldudki praktiliste näidete varal täienduseks matemaatika õppijatele.

Standardid

Kuna tänapäeval muutuvad suured koostööprojektid ja ehitised üha enam ka rahvusvahelisteks objektideks, siis on ka väga oluline, et jooniseid (projekti) vaadates kõik asjadest ühtemoodi aru saaksid, kuna igasugune joonestatud projekt sisaldab ka hulgalised kokkuleppelisi tähendusi ja tingmärke (leppemärke).

Selleks on loodud selguse huvides rahvusvaheline standard (ISO – the International Organization for Standardization), kuid nende kõrval kehtivad ka kohalikud rahvuslikud standardid, mis reguleerivad ehitajate ja tellijate vahelist koostööd kohapealses riigis. Samuti on olemas Euroopa Liidu standardid (EN) ning Eesti Vabariigi standardid (EVS – Estonian Centre for Standardization).

Standardite eesmärgiks on kõigile üheselt teha arusaadavaks ehitus- või tootmisprotsessis käsitletavad seadused, mõisted ja reeglid.

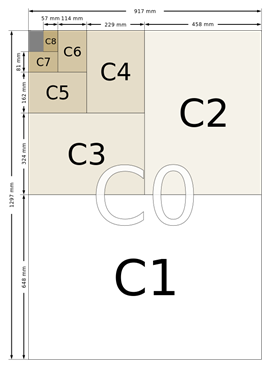
Jooniste ja paberformaadi juures on üheks tuntumaks standardiks ISO 216. Selle standardi alusel määratletakse ära 3 paberisuuruse formaati A, B, C. C- seeria on kasutusel kirjaümbrikute juures. Paberisuuruste standard võeti esmakordselt kasutusele 1922. aastal Saksamaal. Saksa standardi järgi on see DIN 476. Need on muutunud rahvusvaheliseks meetermõõdustiku süsteemiks, kus jooniste ühtsed mõõdud annavad ühise arusaama kasutatavate jooniste täpsetest suurustest ja mõõtudest. Nagu all oleval joonisel näha võib, kasutatakse paberformaadi suuruste iseloomustamiseks tähte A, B või C ja selle taga olevat numbrit.
A-seeria lühema külje suhe on pikemaga 1:√2 . Teatavasti on √2 irratsionaalarv (ümmardatult 1:1,4142). Saadud küljepikkuse tulemus ümmardatakse täismillimeetriteni. Kõige laialdasemalt on tuntud kirjapaberi A4 formaat 210 x297.

Teatavasti saab ruudu diagonaal pikkust väljendada

. Seda sama põhimõtet kasutatakse samuti paberi A formaadi laiuse ja kõrguse suhte tuletamiseks.

Näiteks, kui võtta formaat A4, kus a = 210 mm, siis

= 296, 98 ≈ 297 mm

Arvutikasutajana oleme kohanud, et inglise keelses maailmas kasutatakse väljaprintimisel sellele ligilähedast „Letter“ formaati, mille mõõdud on 216 x 279.
Tähe taga olev number aga iseloomustab kindalt suurust ehk formaati. Kõige väiksem number on 0, aga ühtlasi on see kõige suurem formaat, mille mõõdud on 841 x 1189 mm. A0 on määratud põhimõttel, et selle formaadi pindala on 1 m2.
Iga järgnev number pikemast küljest 2 korda (ehk poole) väiksem suurus.

B – seeria mõõdud on geomeetrilised keskmised A – seeria ühe võrra väiksemast numbrist. B1 suuruse saamiseks on võetud geomeetriline keskmine A1 ja A0 mõõdust.
C – seeria tuletamiseks on võetud A – seeria ja B – seeria sama numbri mõõtudest. Näiteks C2 suurus on saadud A2 ja B2 keskmistest mõõtudest.
C 4 ümbrik on mõeldud A4 suuruse kirjapaberi jaoks. Kui murrame A4 kirjapaberi keskelt pooleks, saame suuruseks A5, mis mahub C5 suuruse ümbrikku sisse.

	A-	B-	C-
0	841 × 1189	1000 × 1414	917 × 1297
-1	594 × 841	707 × 1000	648 × 917
-2	420 × 594	500 × 707	458 × 648
-3	297 × 420	353 × 500	324 × 458
-4	210 × 297	250 × 353	229 × 324
-5	148 × 210	176 × 250	162 × 229
-6	105 × 148	125 × 176	114 × 162
-7	74 × 105	88 × 125	81 × 114
-8	52 × 74	62 × 88	57 × 81
-9	37 × 52	44 × 62	40 × 57
-10	26 × 37	31 × 44	28 × 40

Allikas: Standard ISO 216

Toome näite geomeetrilise keskmise arvutamisest. Kõigepealt vaatame geomeetrilise keskmise valemit.

See on:

Tuletame formaadi B1 mõõdud A0 ja A1 kaudu.

Näiteks külgede 841 mm ja 594 mm geomeetriline keskmine on:

= 706.79 mm ≈ 707 mm

Ja külgede 1189 mm ning 841 mm geomeetriline keskmine on:

= 999.97 mm ≈ 1000 mm

Seega B1 tuletatud mõõdud on 707 x 1000 mm.

Geomeetrilise keskmine on seotud tavaliselt jadadega. Antud näite puhul muudeti mõlema formaadi suurust proportsionaalselt ühepalju.
Sellist arvutusvõimalust on kasutatud ka kino ja TV ekraanisuhte suuruste kompromissvariantide välja arvutamiseks.

Geomeetrilise keskmise graafiline kujutamine on näiteks analoogne kolmnurga kõrguse teoreemiga ja näeks välja nii:

Jooniste juures kasutatakse samuti veel kirja standardeid.
Igapäevaelus on kasutuses aga tuhandeid standardeid. Sõltuvalt majandusharust, näiteks masinaehitusetööstuse standardid, keemiatööstuse standardid jne.

Rahvusvahelised mõõtühikud

Näiteks enne meetermõõdustiku (mõõtühikute) rahvusvahelist kasutusele võtmist olid igal riigil erinevad mõõdusüsteemid, mis tekitasid palju segadust. Nüüdseks aga suurem osa riikidest ühtse rahvusvahelise süsteemi kasutusele võtnud, mis on oluliselt lihtsustanud omavahelist suhtlemist ja asjaajamist.

Ühtsed kvaliteedinõuded

Teise näitena võib tuua olukorra, kus kohalikul tasandil võib tekkida hulga erinevaid arusaamu mõne valminud toote, detaili või ehitise kvaliteedi osas. Kui aga tegevuse käigus on võetud aluseks standard või seadus, mis kirjeldab kvaliteedinõudeid, siis peaks olema see kõikidele osapooltele üheselt arusaadav.

Joonised ja projektid

Joonised

Joonistega tutvumisel vaja alustada kõigepealt endale tingmärkide selgeks tegemisega. Mõningatel joonistel ja plaanidel (looduslikud tingmärgid) on ära toodud ka tingmärkide seletus. Kuid joonise paremaks mõistmiseks on neid kasulik juba eelnevalt teada.

Samas kasutatakse erinevaid standardeid näiteks ehituse ja masinaehituse joonistel. Nende erinevus seisneb joonte liikides, mõõtude jooniste peale kandmises ja tingmärkides.

Kuna ehitajatel tuleb vahel kokku puutuda ka masinaehitusjoonistega, siis sellest tulenevalt on antud valdkonna inimestel kasulik teada mõlema standardi mõisteid ja tähistusi.

Ehitusprojektid

Kui aga defineerida ehitusprojekti, siis see on vajalike dokumentide kogum, mis koosneb seletuskirjast, tehnilistest joonistest, ohutustehnilistest juhenditest, kasutamis- ja hooldusjuhenditest ja muudest asjakohastest dokumentidest.

Mõõtkava ehk mastaap

Matemaatilise poole pealt on üheks oluliseks osaks projekteerimise juures mõõtkava.

Mõõtkava on suurus, mille kaudu on võimalik kanda reaalset olukorda paberile. Näiteks situatsiooni looduses, mõnda planeeritavat ehitist või seadet, samuti mõnda ehitise või seadme juurde kuuluvat detaili.

Mõõtkava kaudu saab suurenda või vähendada tegelikku olukorda. Näiteks ehitised ja hooned on tavaliselt nii suured, et nende kujutamiseks joonistel on vaja nende mõõtusid proportsionaalselt vähendada.

Vastupidine on olukord aga väikeste detailidega. Näiteks mõne väiksema kruvi või seibi kujutamiseks on teda paberile kandes mõistlik suurenda, et oleks võimalik lisada kõikvõimalikke tähistusi ja mõõtusid normaalselt loetavas suuruses.

Tavaliselt väljendatakse projektil, joonisel või kaardil olevaid joone pikkusi kindla suurusena. Joonepikkuseks on valitud kindel suhe kujutatava eseme tegelikku pikkusesesse.

Selleks kasutatakse arvmõõtkava, selgitavat mõõtkava ja topograafias graafilist joon- ning põikmõõtkava.

Ehitusvaldkonnas kasutatakse plaani- ja kaardimõõtu. Vastavat mõõtu ehitusplaanil (projekt) nimetatakse plaanimõõduks. Looduslike suuruste tähistamiseks kasutatakse aga kaardimõõtu, mille kaudu on võimalik tähistada hoone või ehitise suurusi kaardil.

Näiteks plaanimõõt 1:100 tähendab seda, et 1-le pikkusühikule plaanil vastab 100 ühikut tegelikkuses. Mõõt 1:50 on see, kus 1cm vastab tegelikkuses 50 cm ehk 0,5 m.

Näiteks kui kaardil on mõõtkava 1:100 000, siis tähendab see seda, et looduses vastab kaardile 100 000 cm. Kui mõõtühikud teisendada, siis 100 000 cm = 1000 m = 1 km. Siit saame järeldada, et kaardil 1 cm pikkusele lõigule vastab looduses 1 km, ehk kui meil on 5 cm lõik kaardil, siis looduses vastab sellele 5 km.

Eeloleva teisenduse saime järgmisel moel 1 km = 100 cm x 1000 cm = 100 000 cm

Mõõtkava liigid

Arvmõõtkava Näiteks 1:500. Selle mõõtkava järgi saab arvutada pikkusi plaanil ja maastikul
Joonmõõtkava. Joonmõõtkavas saab mõõtmisi teostada mõõtsirkliga. Sirkli haarade vaheline lõik kaaril on joonmõõtkavale asetades joone pikkus looduses.

Põikjooneline- ehk transversaal mõõtkava. Põikmõõtkava juures tehakse mõõtmisi samuti sirkliga. Täiendavaks võimaluseks on siin mõõtkava kõrgus, kus põhiühikud jaotada väiksemateks ühikuteks; kümnendikeks ja sajalisteks.

Mõõtkava täpsus

Vähim pikkus, mida võib näha plaanidel ja kaartidel näha lõiguna on 0,2mm.

Harjutusülesanded mõõtkava kohta

Teisenda mõõtekava võrdlusmõõtkavaks, samuti tee vastupidi.

a. 1 : 10 000

b. 1 cm – 20 km

c. 1 : 500

d. 1 cm – 600 m

e. 1 : 1000

Test

Harjutustest

Mõõtmine tollimõõdus

Mõõtühikud

Kuigi meie mõõtühikute süsteem on SI-süsteemis ehk meetermõõdustikus (kümnendsüsteemis) on vahel osaliselt kasutusel mõningates ehitusvaldkondades tollimõõdud. Üks valdkond, kus tollimõõtu üsna tihti kasutatakse on puusepa valdkond. Kõige rohkem esineb seda puitmaterjali kasutamisel. Samuti kasutatakse tollimõõtu torutöödel. Puitmaterjali ja torude mõõdud on sageli antud tollides.

Seepärast vaatleme natuke ka tollimõõte.

Varasematel aegadel, kui ei olnud veel ühtsed rahvusvahelised mõõdusüsteemid välja töötatud, kasutati mõõtmisel kehaosade pikkusi. Teatavasti võis see aga kõikuda üsna suurtes piirides, mis tekitas omakorda palju segadust.

Näiteks norra-taani tolli pikkuseks oli 26,2 mm rootsi tollimõõt vastas 24,7 mm pikkusele ühikule. Samuti erinevad teatud valdkondades ameerika ja inglise mõõdusüsteemid.

Praeguseks on meil välja kujunenud nii, et

1 toll (1”) = 25,4 mm

1 jalg (1’) = 12 tolli (12“) = 304,8 mm

1 küünar = 21 tolli (21”) = 533 mm

Torunäidised

Puidust plank

Kümnendsüsteemi ehk meetermõõdustiku kasutamisel on tollimõõdustikust erinevad suuruste täpsusastmed. Kui kümnendsüsteemis me väljendame täisarvust väiksemaid suurusi kohtade arvuga peale koma. Näiteks 0,1; 0,01; 0,001 jne. Tollimõõdus muutuvad täpsusastmed murdude lõikes.